
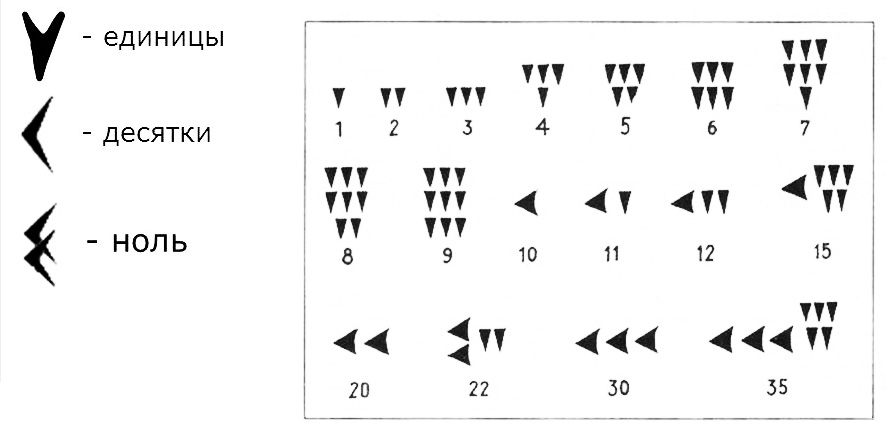
Строго говоря, для вычислений нужно всего два значка: «ноль» и «единица». С единицей проблем не было никогда. Один предмет и единица как его представитель. А вот с нулём дело обстояло куда сложнее. Много тысяч лет в вычислениях обходились вообще без нуля. Правда, при таком подходе задача «было два яблока, отдали одно — сколько осталось?» решалась просто (II отнять I будет I), а вполне себе жизненная задача «было два яблока, отдали два — сколько осталось?» позволяла решение записать (II отнять II), а вот что будет результатом, оставалось неясным. Средств записи «ничего не будет», «ни одного» или «нисколько» не предусматривалось. И была (даже раньше) задача, как записать в позиционной системе число, в котором не было ни одной единицы в конкретном разряде.
Появление нуля, видимо, и было в первую очередь связано с необходимостью иметь местоблюститель позиции, в которой нет ни одной единицы (запись 207 означает две сотни, ни одного десятка и семь единиц, и без местоблюстителя десятков записать это число нельзя).
Получится либо «2 7», либо 27, но тут о сотнях ничего не говорится. И понять, что местоблюститель (0 как цифра) и 0 как число — это одно и то же, оказалось задачей нетривиальной, на решение которой ушли столетия. Есть и другие определения нуля, и о некоторых мы поговорим в этой статье.
В Европе (Россия, Греция, Рим) счёт был непозиционным. Единица обозначалась вертикальной чертой, для степеней десяти (10, 100, 1000 и т.п.) использовались отдельные значки. Если какого-то разряда в числе не было, то его просто не писали.
На Руси использовали так называемый ясачный счёт для записи налоговых платежей (ясак со времён Чингиз-хана это и есть налог). Это был упрощённый счёт на небольших объёмах вычислений.

На больших объёмах использовали буквенные литеры со специальными значками над литерой (надчерки) в виде тире, крышечек или тильды (волнистое тире). Сути это не меняло, но вместо единственной цифры (единица, десяток, сотня) появлялись отдельные цифры от одного до десяти (строго говоря, до девяти, т.к. десять единиц текущего разряда тут же превращались в одну единицу следующего разряда). При массовых и сложных вычислениях так было легче. Ясачный счёт был проще и быстро осваивался теми, кто алфавита не знал.
То, что называют римской системой счисления, прошло длинный путь и существует в нескольких вариантах.
Параноидально строгая римская система состояла из символов I (единица), X (десять) и C (сто). Для записи больших чисел использовался надчерк. Один надчерк увеличивал вес числа в тысячу раз. Два надчерка — в миллион, а три надчерка — в миллиард раз. Для записи I с надчерком (тысяча) использовался внесистемный символ M (тысяча). Иногда использовался символ Z для двух единиц с надчерком (две тысячи). Для повышения производительности вычислений в этой системе использовались расчерченные линии (это и называлось «счёт на линиях». Линии можно было расчерчивать на мокром песке, но вполне можно было делать каменные счётные доски, на которые линии были нанесены в виде канавок), либо — так называемый греческий абак, где под разряды выделялся столбик в ящике счётной доски, в который клали от 1 до 9 камушков. Если столбик оставался пустой, то в соответствующем разряде ничего не было, и в результирующей записи соответствующих цифр просто не было. В отличие от счёта на линиях (временные линии на песке или стационарные линии на счётной плите) абак был носимым счётным прибором.

Прагматичная римская система делила десяток на пятёрки, что позволяло упрощать запись (для пяти единиц использовали V, для пяти десятков использовали L и для пяти сотен использовали D — символа для пяти тысяч я найти не сумел, хотя и не исключаю, что такой был). Число записывали цифрами в любом порядке, но принято было писать слева направо от больших весов к меньшим. Надчерки по-прежнему увеличивали вес числа в тысячу раз. В римских абаках использовалась именно такая прагматичная система. Правда, числа получались длинные (LXXXXVIIII для «девяносто девять»), но это было именно то, что показывал римский абак: усовершенствованная версия греческого абака с прорезями и шариками вместо камешков; в верхнем ряду ставят пятёрки тех единиц, которые ставят в нижнем ряду.

Интересна разметка под тысячью. Вместо надчерков используется M как суффикс (M или I с надчерком обозначает тысячу, XM или десять с надчерком обозначает десять тысяч, CM или C с надчерком означает сто тысяч, MM или I с двумя надчерками обозначает миллион).
Для сокращения записи использовали правило мелких нарушений порядка. Единица слева от пятёрки означала «пять минус один» или четыре, единицы справа прибавлялись к пятёрке (получалось шесть, семь или восемь. То же самое касалось десятки. Единица слева вычиталась, а единицы справа прибавлялись (т.е. первые числа от 1 до 50 были I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII, XIII, XIV, XV, XVI, XVII, XVIII. XIX,XX XXI, XXII,XXIII, XXIV,XXV, XXVI, XXVII, XXVIII, XXIX, XXX, XXXI, XXXII, XXXIII, XXXIV, XXXV, XXXVI, XXXVII, XXXVIII. XXXIX, XL, XLI, XLII, XLIII, XLIV, XLV, XLVI, XLVII, XLVIII, XLIX, L). К слову, именно эти мелкие нарушения порядка препятствовали письменным вычислениям «в столбик».
Аналоги римского абака существовали в Китае (суанпань) и Японии (соробан), но в них вместо желобка использовалась проволока, по которой перемещались жетоны. По аналогичной технологии (жетоны на проволоке) были устроены русский прибор сошного счёта (соха — это единица налоговых вычислений) и русские счёты, но они имели по десять жетонов в ряд, т.е. были аналогом не римского, а греческого абака.
Как видим, непозиционные системы счисления позволяют обходиться без местоблюстителя отсутствующего разряда за счёт того, что для каждого разряда используются отдельные символы. В Вавилоне работали с глиняными табличками и в качестве инструмента использовали стило, которое позволяло нарисовать либо «галочку» (вертикальную или горизонтальную) либо «жирную точку» (если повернуть стило). В этих условиях возможность использовать разные символы для разных разрядов отсутствовала, и система счисления становилась позиционной («вес» разряда увеличивался справа налево). Для записи единиц использовались вертикальные галочки (от одной до девяти). Поскольку система счисления была шестидесятеричной, то для сокращения записи разряда использовали горизонтальные галочки (каждая соответствовала десяти вертикальным галочкам). В качестве местоблюстителя отсутствующего разряда использовалась либо жирная точка, либо сдвоенная горизонтальная галочка.
Следы шестидесятеричной системы мы видим в измерении времени (часы, минуты, секунды) и координаты (градусы и минуты с секундами).
Если уменьшить вес разряда (перейти к десяти- или двенадцатеричной системе счисления) и придумать отдельное обозначение для каждой цифры, то получается вполне комфортная среда для письменных вычислений «в столбик». Одним из вариантов такой системы является арабская (ставшая общепринятой). Чтобы мнемонически легче было запомнить, величина цифры соответствует количеству углов.
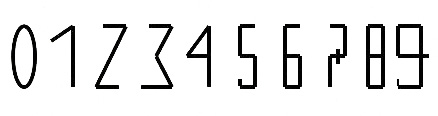
Вавилонская система — это третье тысячелетие до н. э., а римская — первое тысячелетие до н. э., т.е. идеологически более сложная позиционная система появилась раньше, чем куда как более примитивная римская система счисления. Гипотез тут две. Либо в истории человечества действительно были периоды регресса, когда терялись знания и навыки, либо так сильно сказывался тот факт, что в Вавилоне носителем была глина, что ограничивало изобразительные возможности. А в Средиземноморье (в т.ч. в арабском мире и в Риме) применялась кожа, папирус (позднее бумага), что позволяло использовать гораздо больше изобразительных возможностей.
Видимо, самым древним (уцелевшим) письменным памятником, в котором обсуждается проблема нуля, является хранящийся в библиотеке Оксфорда «манускрипт Бакхшали». Он неполон и состоит из листов бересты. Судя по всему, первоисточник был создан в самом начале первого тысячелетия н. э., а в библиотеке Оксфорда хранится список, сделанный на несколько веков позже. Из дошедших до нас письменных памятников этот манускрипт — первый, в котором ноль упоминается как местоблюститель (как и в Вавилоне для этого используется «жирная точка»). Специалисты относят (не подтверждённое письменным источником) применение нуля как местоблюстителя несуществующего разряда к V—VI веку до н. э.
Самый старый трактат, в котором ноль употребляется и как цифра (местоблюститель разряда), и как число, — скорее всего, «Брахма-спхута-сиддханта» («Усовершенствованное учение Брахмы», VI—VII век н. э.). Здесь же появляется ноль и в третьем значении — как начало отсчёта числовой оси с положительными и отрицательными числами. Это уже третье определение нуля.

Четвёртым определением нуля, видимо, является его применение в математической логике (в исчислении алгебры логики 0 трактуется как ложь, а 1 как истина). В интерпретации логических схем 0 трактуется как «разомкнуто», а 1 как «замкнуто», и в этой интерпретации также действует алгебра логики.
История нуля показывает, что очень часто величайшие результаты, которые определяют развитие на тысячелетия вперёд, даются столетиями трудов величайших учёных, а потомками воспринимаются как самоочевидное. И действительно, что может быть проще нуля, когда уже выяснили, что это такое и когда ноль стал одним из столпов математики! Что ж, работа проделана, но на это ушло много столетий, когда никто не хотел верить тем, кто узрел новое и попытался его осознать и внедрить в практику… Но это, впрочем, так естественно для человечества. Ведь и вся история цифровых технологий развивалась по этой «схеме». Столетия «цифра» была на задворках техники, а сегодня куда ни взглянешь — везде «цифра»!
И это нормально. Мелкие улучшения защищаются копирайтом (патентами) потому, что у каждого из них можно вычленить авторов и определить их роль, а у гениальных базовых результатов авторов так много и они так распределены по времени, что ни авторства, ни приоритета не установишь… А представьте на минуточку, что ноль удалось бы запатентовать, и тысячелетиями все, кто его используют, платили бы роялти… Вот это и есть признак величайшего результата. Нет патентов, нет авторов, и роялти получать некому… И любая попытка запатентовать наталкивается на ответ: «это общеизвестно».



